Jak znaleźć obszar trójkąta równoramiennego

Matematyka i geometria w szczególności, wedługsondaże uczniów, jedna z najbardziej niekochanych lekcji, a wszystko dlatego, że uczą cię ogromnej liczby formuł, że w życiu 90% obecnych dorosłych nie znalazło praktycznego zastosowania. Ale przez chwilę uczymy się formuł, rozwiązujemy problemy, tworzymy równania nie dlatego, że mogą nam się przydać w życiu, ale dlatego, że rozwijają myślenie i logikę. Nawet starożytni mędrcy greccy mówili, że ludzki intelekt można zmierzyć dzięki znajomości matematyki. A ponieważ zdecydowałeś się zapoznać z zastosowaniem formuł dla trójkąta równoramiennego - bierzemy się za rękę i czytamy cały artykuł.
Zanim zaczniesz odpowiadać na pytanie, jak znaleźćw obszarze trójkąta równoramiennego i przejdź do praktycznej części artykułu, gdzie podano formuły i obliczenia, określmy samą koncepcję dla siebie. Trójkąt równoramienny jest trójkątem, w którym dwa z trzech boków mają równą długość, zwane bokami bocznymi. W przypadku regularnego trójkąta, w którym wszystkie strony są równe, jest on również uważany za równoramienny, ale na odwrót, kiedy trójkąt równoramienny jest uważany za poprawny - jest fałszywy.
Boki trójkąta powinny być wyznaczone, zrobimy to w ten sposób, jak pokazano na rysunku poniżej, gdzie: a - boki, b-podstawa i h-wysokość.
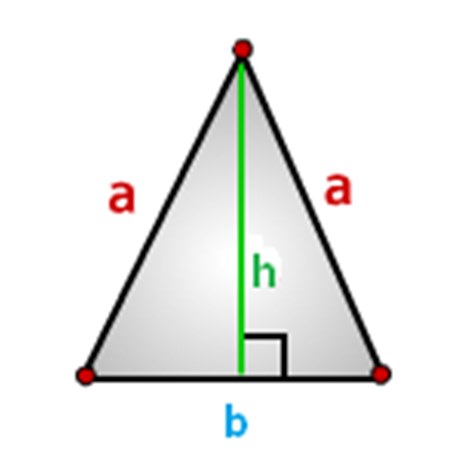
Jak obliczyć obszar trójkąta równoramiennego, formuły.
Po dokonaniu zapisu wysokości, boków i kąta możemy zacząć rozwiązywać problem.
Na początek określimy to, co wiemy.
Jeśli wysokość i dół - to klasyczna formuła (* - znak mnożenia):
S = ½ * b * h
Zamieńmy na przykład liczby gdzie: h = 16, b = 18, otrzymujemy:
S = 1/2 * 18 * 16 = 9 * 16 = 144;
Powierzchnia trójkąta równoramiennego wynosi S = 144 cm2
Są inne formuły, które nam pomogąw jaki sposób poznać obszar trójkąta równoramiennego. Jedną z takich formuł jest metoda Herona. Nie piszmy skomplikowanej formuły, przyjmujemy, na podstawie, skróconą:
S = ¼ b √4 * a2-b2
Oczywiste jest, że b jest podstawą i - równymi stronami. Wzór jest odpowiedni w przypadku, gdy wysokość h jest nieznana.
Po podstawieniu wartości, niech a = 6, b = 3, otrzymujemy:
S = ¼ * 3 √ 4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Możesz użyć do obliczenia powierzchni równej bokom trójkąta i kątowi pomiędzy bokami:
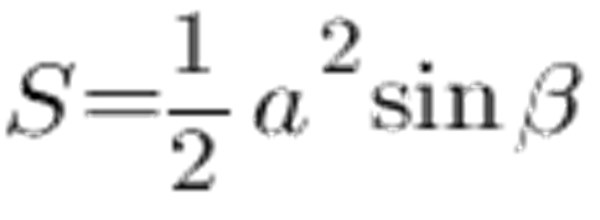
Zgodnie z tabelą sinusoidalną kąt 45 ° wynosi 0,7071, a bok a 6 cm, otrzymujemy co następuje:
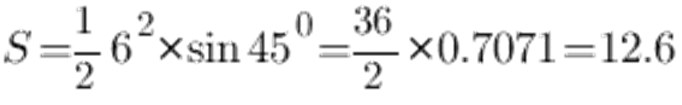
W rezultacie powierzchnia trójkąta równoramiennego wynosi 12,6 cm2.
Istnieją również sposoby obliczania obszaru, w tymw tym przypadku trójkąta równoramiennego, ale są one dość skomplikowane i nie mają zastosowania do "elementarnych" obliczeń, takich jak te podane powyżej, w pojęciu złożonej matematyki. I nie warto mówić o rzeczach, których nawet nauczyciele z doświadczeniem nie zrozumieją.
Więc możesz odetchnąć z ulgąmały przebieg geometrii dla znalezienia obszaru trójkąta równoramiennego zostanie uznany za kompletny, a wiedzę uzyskaną w wyniku czytania artykułu nauczy się przez "pięć".














